Pub

Interval and Skyline Problem

By: Homecox. 12/13/2013

The Skyline problem is like this: Given a series of building's position and height (start, end, height), return the combined skyline.

Alternative description can be: given n speakers S1, S2, ... Sn, each has different volumn at different time period, return every time period and the max volumn ini each time period. E.g.,

S1: {[2,5], vol=10}, {[6,10], vol=2}
S2: {[1,6], vol=1}, {[8,12], vol=8}

For S1 and S2, the output will be: [1,2],vol=1, [2,5], vol=10, [5,6], vol = 1, [6,8], vol = 2, [8,12], vol = 8.

People who have worked on Merge Interval and Insert Interval questions may immediately feel this is similar, and solution may be obtained by extending the solution to the interval problems.

The Merge Interval problem is: given a series of intervals (start1, end1), (start2, end2), ..., merge them such that there is no overlap between resulted intervals.

A solution to the merge interval problem is given below. First we sort the intervals using the start value. Then, each round we look at the first 2 intervals: 1) if no overlap, add the first to result set, 2) if the first overlaps the second but not longer than the second, we merge the first into the second, 3) if the first overlaps the second and is longer than the second, we also merge the two.

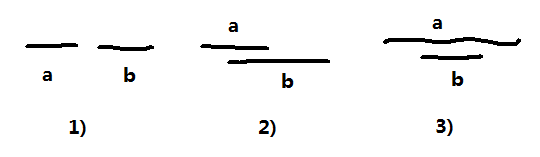
Each round we can remove exactly one interval, so the algorithm ends, with the correct result. Obviously, this is a nlog(n) algorithm.

    vector<Interval> merge(vector<Interval> &intervals) {
        vector<Interval> ans;
        if (intervals.size() == 0) return ans;
        
        sort(intervals.begin(), intervals.end(), comp);
        
        while (1) {
            if (intervals.size() == 1) {
                ans.push_back(intervals[0]);
                return ans;
            }
            
            Interval &a = intervals[0];
            Interval &b = intervals[1];
            
            if (a.end < b.start) {
                ans.push_back(a);
            }
            else if (a.end <= b.end) {
                b.start = a.start;
            }
            else {
                b.start = a.start;
                b.end = a.end;
            }
            intervals.erase(intervals.begin());
        }
    }

Now, to solve the Skyline problem, we have one more dimension, the height, this complicates the merge process a little bit, but the idea is the same. Look at the graphs below.

The code solution is given below.

    vector<Interval> merge(vector<Interval> &intervals) {
        vector<Interval> ans;
        if (intervals.size() == 0) return ans;
        
        sort(intervals.begin(), intervals.end(), comp);
        
        while (1) {
            if (intervals.size() == 1) {
                ans.push_back(intervals[0]);
                return ans;
            }
            
            Interval &a = intervals[0];
            Interval &b = intervals[1];
            
            if (a.end < b.start) {
                ans.push_back(a);
            }
            else if (a.end <= b.end) {
                if (a.height == b.height) {
                    b.start = a.start; // merge a into b.
                }
                else if (a.height < b.height) { // split.
                    a.end = b.start;
                    ans.push_back(a);
                }
                else { // a.height > b.height
                    b.start = a.end;
                    ans.push_back(a);
                    sort(intervals.begin(), intervals.end(), comp);
                }
            }
            else {
                if (a.height >= b.height) {
                    b.start = a.start; // merge b into a.
                    b.end = a.end;
                }
                else { // split.
                    Interval c(b.end, a.end, a.height);
                    a.end = b.start;
                    ans.push_back(a);
                    
                    intervals.push_back(c);
                    sort(intervals.begin(), intervals.end(), comp);
                }
            }
            intervals.erase(intervals.begin());
        }
    }

So here, we basically using the same method as Merge Interval. To keep the order property of the input intervals, we need to sort the interval list each time. This is nlog(n) + n*nlog(n) complexity, the first factor is for initial sorting, and the second for n cycles, each cycle nlog(n) for sorting involved. To speed it up, we can use a heap to maintain the order property of the input interval list more effeciently. The solution is given below.

    vector<Interval> merge(vector<Interval> &intervals) {
        vector<Interval> ans;
        if (intervals.size() == 0) return ans;
        
        priority_queue<Interval, vector<Interval>, comp> q;
        
        for (int i = 0; i < intervals.size(); ++ i) {
            q.push(intervals[i]);
        }
        
        while (1) {
            if (q.size() == 1) {
                ans.push_back(q.top());
                return ans;
            }
            
            Interval a = q.top(); q.pop();
            Interval b = q.top(); q.pop();
            
            if (a.end < b.start) {
                ans.push_back(a);
            }
            else if (a.end <= b.end) {
                if (a.height == b.height) {
                    b.start = a.start; // merge a into b.
                }
                else if (a.height < b.height) { // split.
                    a.end = b.start;
                    ans.push_back(a);
                }
                else { // a.height > b.height
                    b.start = a.end;
                    ans.push_back(a);
                }
            }
            else {
                if (a.height >= b.height) {
                    b.start = a.start; // merge b into a.
                    b.end = a.end;
                }
                else { // split.
                    Interval c(b.end, a.end, a.height);
                    a.end = b.start;
                    ans.push_back(a);
                    
                    q.push(c);
                }
            }
            q.push(b);
        }
    }

The complexity of this solution is now nlog(n) + nlog(n) = nlog(n).